Multiphase Flows in Porous Media
Multiphase flows in porous media occur in the production of hydrocarbons from reservoirs, or in the clean-up of contaminated groundwater sites. The mathematical models are coupled nonlinear systems of partial differential equations that are challenging to solve. Some numerical challenges are: heterogeneity of the porous media, degeneracy of the relative mobilities and mass transfer between phases. For instance, absolute permeability can vary over several orders of magnitude in a geological formation.
COMP-M has developed high order and locally mass conservative methods for incompressible two-phase, three-phase and black-oil models. Our publications show the advantages of using discontinuous polynomial approximations of high degree. The spatial discretization is based on interior penalty discontinuous Galerkin methods, or on hybridizable discontinuous Galerkin methods. For time stepping, we have compared sequential and fully implicit formulations. For two-phase flow, we have analyzed and implemented several schemes using any combination of wetting and non-wetting phase pressure and phase saturation. Our method for solving black-oil uses for primary unknowns, the liquid phase pressure, the aqueous phase saturation and the total mass fraction of gas component.
Convergence of FEM solution for degenerate two-phase flows
The numerical analysis of two-phase flows in porous media is challenging because of (i) the degeneracy of the relative permeabilities in the elliptic parts of the equations and (ii) the unboundedness of the closure models for the capillary pressure. Practitioners prefer to use numerical schemes that solve for physical quantities, such as phase pressure and phase saturation. Therefore the use of the artificial global pressure to remove the degeneracy in the schemes is not permitted. We formulate and prove convergence of a finite element method with mass lumping for solving the incompressible
two-phase flows. The proof is based on a compactness argument. To our knowledge, this is the first theoretical convergence result of a variational-based method for degenerate two-phase flows.
This project is funded by NSF: grant NSF-DMS 1913291.
V. Girault, B. Riviere and L. Cappanera. A Finite Element Method for Degenerate Two-Phase Flow in Porous Media. Part I: Well-Posedness, Journal of Numerical Mathematics, 29 (2), p.81–101, doi: 10.1515/jnma-2020-0004, 2021.
V. Girault, B. Riviere and L. Cappanera. A Finite Element Method for Degenerate Two-Phase Flow in Porous Media. Part II: Convergence, Journal of Numerical Mathematics, 29 (3) p.187–219, doi: 10.1515/jnma-2020-0005, 2021.
Elimination of overshoot/undershoot in saturation for two-phase flows
Overshoot and undershoot phenomena in discontinuous Galerkin methods are small oscillations localized in the neighborhood of a front in a convection-dominated problem. There are several ways to reduce the amount of overshoot/undershoot: implicit time-stepping, local grid refinement, magnitude of penalty parameter and limiters. These local oscillations remain small and bounded throughout the simulation in the best case scenarios. They are however never eliminated.
Our work on flux limiters addresses this challenge for DG methods applied to two-phase flows in heterogeneous media. In the case of incompressible two-phase flows, we prove that the numerical saturation is guaranteed to satisfy the maximum principle. The combination of flux limiters and slope limiters eliminate the overshoot and undershoot phenomena for realistic simulations.
This project is funded by NSF: grant NSF-DMS 1913291.
M.S. Joshaghani, B. Riviere and M. Sekachev. Maximum-principle-satisfying Discontinuous Galerkin Methods for Incompressible Two-Phase Immiscible Flow, Computer Methods in Applied Mechanics and Engineering, 391, p.114550, doi:10.1016/j.cma.2021.114550, 2022.
Multinumerics DG-FV method for two-phase flows
The DG-FV method is a multi numeric approach that combines the advantages of both discontinuous Galerkin method and cell-centered finite volume method in a non-overlapping domain partition. We propose special discretization of the coupling terms at the interface of the DG and FV subdomains, for the two-phase flow problem in heterogeneous porous media.
This project is funded by NSF: grant NSF-DMS 1913291.
B. Doyle, B. Riviere and M. Sekachev. A Multinumerics Scheme for Incompressible Two-Phase Flow, Computer Methods in Applied Mechanics and Engineering, 370, 113213, doi:10.1016/j.cma.2020.113213, 2020.
Deep Learning Algorithms for Biomedical Image Segmentation
The segmentation and labeling of medical images (CT-scans of tumors in brain, liver, or other organs) is critical in developing optimal treatments. Because the manual segmentation and labeling is time-consuming and expensive, semi-automatic and fully automatic methods are promising techniques that can reduce the time to analyze volumes of data. Our group is developing algorithms based on the formulation of various network architectures (including PocketNet) and the combination of neural networks with numerical solution of the level set equation. This work is done in collaboration with scientists from MD-Anderson Cancer Centre.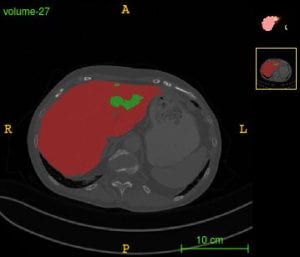
Scientific Machine Learning
The integration of numerical PDEs with neural networks is reducing the computational cost for modeling physical phenomena. We are proposed an unsupervised learning method to solve elliptic problems. The algorithm does not require any training data and it learns an approximation of the finite difference solution to the PDEs.Multidimensional Couplings
The mathematical and numerical analysis of multidimensional (3D-1D) coupled problems is challenging because of the lack of smoothness in the solution. Applications of these coupled problems are many; for instance the mathematical modeling of blood flow in organs is important in understanding the mechanisms of organ perfusion, embolization and drug delivery. This project is funded by NSF: grant NSF-DMS 2111459.Pore-scale modeling
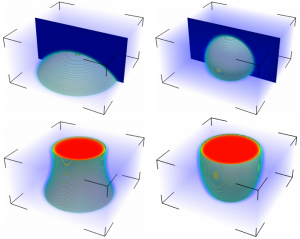Phase-field models are becoming increasingly popular in hydrodynamics for modeling multi-phase fluid flow below Darcy scale. Instead of sharp interfaces, phase transitions appear as diffuse finite-thickness transition regions. The Cahn–Hilliard equation describes phase separation (the alignment of a system into spatial domains predominated by one of the two components) of an immiscible binary mixture at constant temperature in the presence of a mass constraint and dissipation of free energy. It is a stiff, fourth-order, nonlinear parabolic partial differential equation, which may serve as a prototype phase-field problem as intermediate step towards models that take other or additional phenomena into account, e.g., miscibility or multiple components. The wettability characters of the solid surface is reflected by a contact angle between the diffuse interface and the surface.
The Cahn-Hilliard equations are coupled with incompressible time-dependent Navier-Stokes equations to simulate immiscible two-phase flow in the rock at the pore scale.
Incompressible Navier-Stokes
COMP-M has formulated and analyzed interior penalty discontinuous Galerkin methods for solving the incompressible Navier-Stokes equations, both steady-state and time-dependent. We have proved the inf-sup condition for discontinuous polynomial spaces of degree k for velocity and degree k-1 for pressure. We have developed splitting schemes as well as sub grid eddy viscosity schemes. By enriching the discrete space with bubbles, we have obtained a convergent DG scheme that is penalty-free. For all these methods, convergence is obtained by deriving a priori error estimates that are optimal in space and time. We contributed to the development of stable and cheap elements for the Stokes operator by introducing the continuous P1 element with piecewise constants for velocity, combined with piecewise constants for pressure. The resulting method is referred to as the enriched Galerkin method. We have proved stability and convergence of the enriched Galerkin scheme.Our most recent contribution is the analysis of a discontinuous Galerkin pressure correction splitting scheme, that is well suited for large scale simulations. Well-posedness and a priori error estimates are derived.
Modeling hemodynamics and congenital heart defect
COMP-M has developed and analyzed mathematical models of blood flow in whole-body circulatory system that includes major organs and blood vessels, as well as the heart and its valves. The mathematical models have been applied to modeling of single ventricle heart defects, such as hypoplastic left heart syndrome (HLHS). Left untreated, HLHS is fatal. Even with surgical repair, the mortality rate is 15%. Children with HLHS are hemodynamically unstable as a result of mixing between oxygenated and de-oxygenated blood, which often results in cardiorespiratory arrest. We have derived a reduced model for solute transport, that can be used to model the transport of oxygen and carbon dioxide in the circulatory system. We have proposed an efficient numerical solution of the coupled reduced models of flow and transport.Poroelasticity: Coupling Flows and Deformation in Porous Media
Biot's linear poroelasticity model is used to simulate the interactions between fluid flow and deformation of the porous medium (subsurface for instance). In the case of single phase flow in deformable porous media, we have proposed decoupled and sequential numerical methods based on either finite element methods or discontinuous Galerkin methods. Unlike other splitting approaches, our method is not iterative, which results in a speed-up of the computational time. We have obtained a convergence analysis and we have applied the method to large reservoirs.
We have extended the decoupled strategy to the case of immiscible two-phase flows in deformable porous media.
The poroelasticity equations now consist of three coupled nonlinear PDEs, for which the unknowns are the displacement of the solid structure and the two phase pressures.
Miscible displacement
COMP-M has developed efficient algorithms for modeling one-component single-phase flow in porous media. The motion of a miscible fluid through the rock is also called miscible displacement. Modeling this complex fluid flow is crucial to applications related to both Energy and Environment. For instance, production of hydrocarbons is increased by the use of enhanced oil recovery techniques, which is based on the injection of miscible fluids in the reservoirs.
The incompressible miscible displacement problem is governed by a system of nonlinear coupled partial differential equations. The fluid mixture moves as a single phase modeled by Darcy's law. The first equation in the system is the pressure equation. The second equation in the system is a transport equation with a diffusion-dispersion matrix coefficient that depends nonlinearly on the velocity. The unknowns are the fluid mixture pressure and velocity as well as the concentration of the solvent fluid. The miscible displacement problem has several numerical challenges. The equations are coupled via the fluid viscosity for the pressure equation and via the velocity and diffusion-dispersion coefficients for the concentration equation. One important challenge is that the diffusion-dispersion matrix is not bounded, and thus the convergence analysis of the numerical method for the concentration equation is difficult. Most of the published literature on the analysis of algorithms simply assumes that the diffusion-dispersion coefficient is uniformly bounded above, independently of the velocity. In our most recent work, we do not make this boundedness assumption and we refer to this problem as the miscible displacement problem with low regularity. We proved convergence of a high order scheme (both in time and in space) of the numerical solution to the weak solution as the mesh size and time step tend to zero. The underlying discretizations are interior penalty discontinuous Galerkin (IPDG) methods. We also analyzed the scheme combining IPDG and mixed finite element methods.
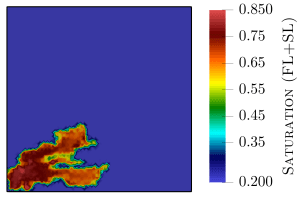
Viscous fingering in porous media characterizes the flow instability phenomenon that occurs when a fluid with low viscosity is used to displace a fluid with high viscosity. As the result of the viscosity difference, a tiny perturbation can be amplified exponentially, which triggers a finger-like pattern in the fluid concentration profile during the fluid displacement. COMP-M has simulated the viscous fingering fluid instability during the miscible displacement process in porous media, on structured and unstructured grids. The numerical model incorporates decoupling in time, discontinuous Galerkin method of high order, flux reconstruction, and parallel implicit solvers to produce an accurate and efficient predictive tool for finger growth. The numerical model does not suffer from grid orientation, accurately measures finger growth rate.
Our publications include discussions on the effect of grid orientation and anisotropic permeability using high order discontinuous Galerkin method in contrast with cell-centered finite volume method. The study of the parallel implementation shows the scalability and efficiency of the method on parallel architecture. We also verify the simulation result on highly heterogeneous permeability field from the SPE10 model.
Coupled free-flows with porous media flows
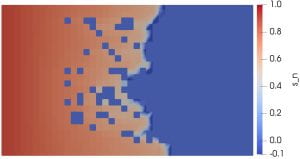
Multiphysics problems are characterized by complex physical processes occurring in different spatial regions. In order to model different physics, the computational domain is subdivided into several subdomains, in which different types of flow and transport phenomena are investigated. The basic mathematical equations are derived from balance equations of continuum mechanics that express conservation laws for mass, momentum, and energy of an arbitrary volume moving with the fluid. Interface conditions are important in capturing the right physics. We assume continuity of normal component of velocity, balance of forces across the interface and the Beavers-Joseph-Saffman condition.COMP-M has developed convergent numerical models that couple free flows with porous media flows. The free flow region is characterized by the steady-state incompressible Navier-Stokes equations whereas the porous media region is modeled by single phase flow. This project helps track pollutants that leak in rivers and lakes and eventually reach groundwater. We proved convergence of various schemes by deriving explicit a priori error estimates; these schemes are the standard IPDG schemes, the classical finite element method and the more recent strongly conservative numerical methods that use divergence-conforming spaces for the fluid velocities. Two-grid solutions are compared with monolithic solutions and we showed that the computational time for the two-grid solution is significantly smaller than the time for the fully coupled solution.
Our group has also obtained existence of weak solutions to these coupled flow problems, for both steady-state and time-dependent cases.
Our most recent contribution to the topic is the formulation and analysis of a numerical scheme for the coupled time-dependent Navier-Stokes equations with single phase flow. The time dependence makes the theoretical error analysis more challenging.
Intestinal edema
Intestinal edema refers to the excess accumulation of fluid in the interstitial spaces of the intestinal wall tissue. This condition can arise in patients with gastroschisis, inflammatory bowel disease and cirrhosis, as well as in patients receiving resuscitative fluid treatments after traumatic injuries. The main problem for a patient with intestinal edema is that the condition causes ileus, a decrease in intestinal transit due to decreased intestinal smooth muscle contractility. Decreased intestinal transit often leads to longer hospital stays and recovery times for patients and in extreme cases can be fatal. The link between edema and ileus is unknown, and is thus the motivation for developing mathematical models to explore this phenomenon. Our numerical model uses the poroelasticity equations and allows for heterogeneities in the intestine, which corresponds to the different layers of the intestine (mucosa, submucosa, muscularis externa, serosa). The rate at which fluid enters the interstitium via the vascular system and the rate at which fluid is removed from the interstitium by the lymphatic system are given by the Starling-Landis equation and the Drake-Laine equation. COMP-M has developed robust numerical models of the intestine, that have been validated by experimental data. New results include an improved view into the effects of resuscitation on the hydrostatic pressure profile of edematous rats, effects on lumenal volume attenuation, relative fluid gain, and an estimation of the impacts of both acute edema, and resuscitation, on intestinal motility.