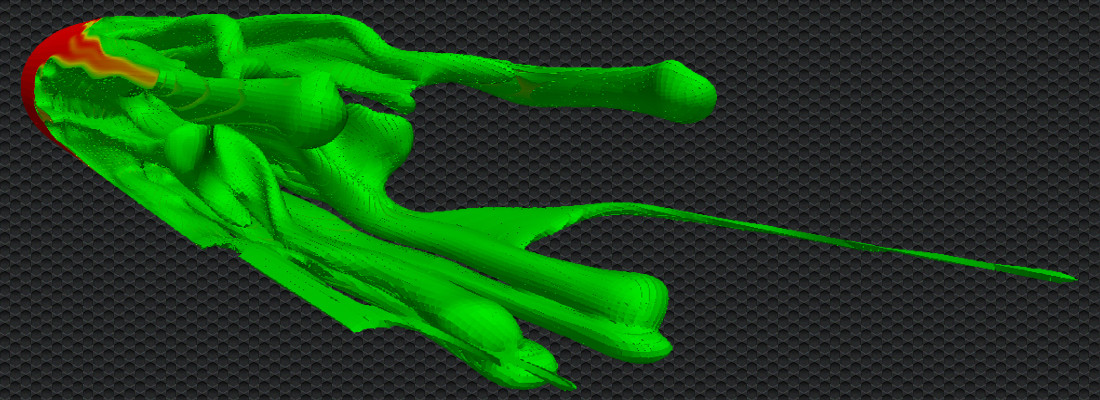
Viscous fingering effect
In miscible system, viscous fluid is triggered by viscous force due to the differences in fluid concentration, also the molecular diffusion and mechanical dispersion of the fluid system.
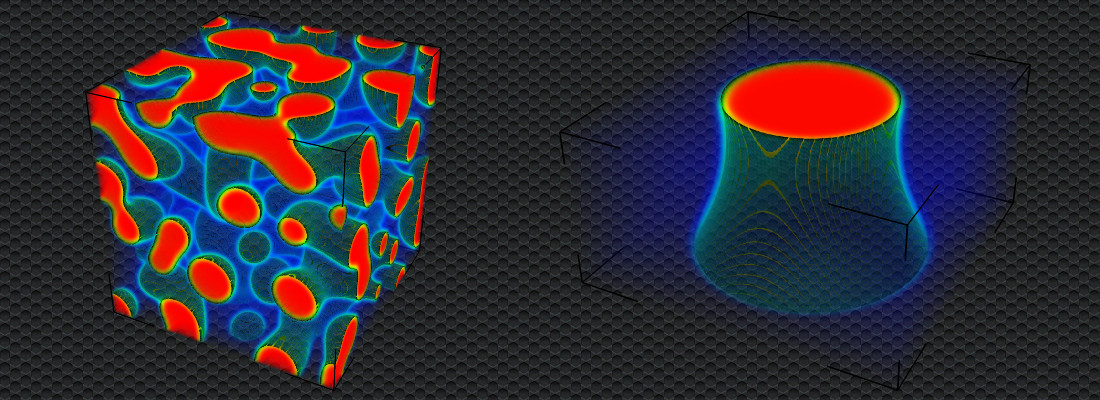
Spinodal decomposition & capillary bridge
Phase-field models are becoming increasingly popular in hydrodynamics for modeling multi-phase fluid flow below Darcy scale. Instead of sharp interfaces, phase transitions appear as diffuse finite-thickness transition regions.
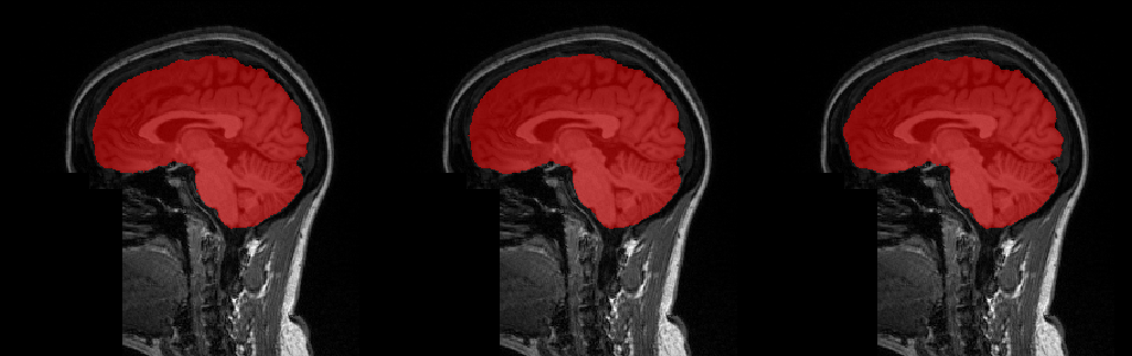
PocketNet: accurate and fast deep learning
We propose the PocketNet paradigm to accelerate prediction with deep learning.
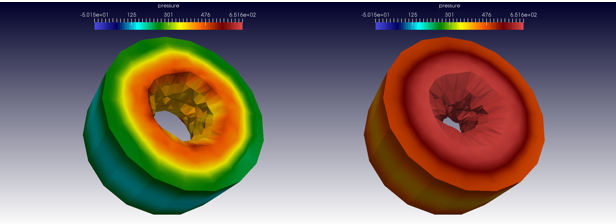
Fluid pressure in 3D section of intestine
Numerical models of intestinal edema help understand the processes behind the decrease of intestinal contractility and ileus.
Direct numerical simulation of fluid flow through Berea sandstone
Pore scale flow modeling enables scientists to predict fluid behavior in a network of pores at the micro-meter scale.
Energy applications: water flooding, enhanced oil recovery, black oil, oil and gas production, pore scale flows, near wellbore modeling
Environmental applications: remediation of contaminated groundwater sites through rivers and lakes, CO2 storage.
Bio-medical applications: single ventricle heart modeling, hemodynamics, oxygen transport in blood vessels, image segmentation of tumors, cell motility, edematous intestine.
Processes in porous media are naturally complex as they relate to various engineering disciplines and span multiple space and time scales. Our research group
Computational Modeling of Porous Media (COMP-M) develops state of the art algorithms for modeling and optimizing physical phenomena occurring in porous media.